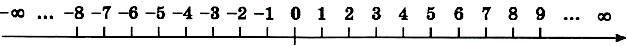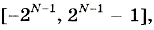Информатика. 10 класс. Базовый уровень. Семакин И.Г., Хеннер Е.К., Шеина Т.Ю. (ФГОС)

Оглавление:
Введение
Введение
Что изучается в курсе информатики для 10—11 классов
Изучение любого школьного предмета можно сравнить со строительством дома. Только этот дом складывается не из кирпичей и бетонных плит, а из знаний и умений. Строительство дома начинается с фундамента. Очень важно, чтобы фундамент был прочным, потому что на него опирается всё остальное сооружение. Фундаментом для курса «Информатика 10-11» являются знания и умения, которые вы получили, изучая курс информатики в основной школе в 7—9 классах. Вам уже не требуется объяснять, что такое компьютер и как он работает; с какой информацией может работать компьютер; что такое программа и программное обеспечение компьютера; что такое информационные технологии. В курсе информатики основной школы вы получили представление о том, в каком виде хранится информация в памяти компьютера, что такое алгоритм, информационная модель. Вы научились обращаться с клавиатурой, мышью, дисками, принтером; работать в среде операционной системы; получили основные навыки работы с текстовыми и графическими редакторами, с базами данных и электронными таблицами. Все эти знания и навыки вам будут необходимы при изучении курса «Информатика 10-11».
Термин «информатика» может употребляться в двух смыслах:
- информатика как научная область, предметом изучения которой являются информация и информационные процессы; в которой осуществляется изобретение и создание новых средств работы с информацией;
- информатика как практическая область деятельности людей, связанная с применением компьютеров для работы с информацией.
Как современная техника немыслима без открытий теоретической физики, так и развитие информатики и информационных технологий невозможно без теории информации, теории алгоритмов и целого ряда других теорий в области кибернетики, лингвистики, семиотики, системологии и прочих наук.
В соответствии с современным пониманием, в информатике можно выделить четыре части:
- теоретическая информатика;
- средства информатизации;
- информационные технологии;
- социальная информатика.
Теоретическая информатика — это научная область, предмет изучения которой — информация и информационные процессы. Как любая фундаментальная наука, теоретическая информатика раскрывает законы и принципы в своей предметной области.
Вторую и третью части в совокупности можно назвать прикладной информатикой. Прикладная информатика — это область практического применения понятий, законов и принципов, выработанных теоретической информатикой. Прикладная информатика, безусловно, связана с применением компьютеров и информационных технологий. В наше время таких прикладных областей очень много: это решение научных задач с помощью компьютера, издательская деятельность, разработка информационных систем, управление различными объектами и системами, техническое проектирование, компьютерное обучение, сетевые информационные технологии и многое-многое другое.
В последние годы в информатике сформировалось новое направление, которое называют социальной информатикой. Его появление связано с тем, что широкое внедрение в жизнь компьютерных технологий и современных средств информационных коммуникаций (Интернета, сотовой связи) оказывает всё более сильное влияние на общество в целом и на каждого отдельного человека. Общественное развитие движется к своей новой ступени — к информационному обществу.
Предметная область современной информатики очень велика и разнообразна. Как известно, нельзя объять необъятное. И наш курс затронет лишь часть тем и задач информатики. Вопросы, которые мы с вами будем изучать, относятся к четырем важнейшим понятиям информатики:
- информационные процессы;
- информационные системы;
- информационные модели;
- информационные технологии.
Правила техники безопасности и гигиены при работе на персональном компьютере
В наши дни персональный компьютер — неотъемлемая часть обеспечения работы, учебы и досуга. Проводя за ним долгие часы, мы не склонны задумываться, что перед нами не только бесценный помощник, но и потенциальный источник повышенной опасности. Этой опасности можно избежать, если соблюдать несложные правила.
Прежде всего, не надо забывать, что компьютер — электроприбор, находящийся под напряжением, величина которого может быть смертельно опасной. Под опасным напряжением находятся и многие отдельные узлы системного блока, а также устройства, составляющие часть рабочего места человека, пользующегося персональным компьютером, — монитор, принтер, сканер, звуковые колонки и т. д. В связи с этим недопустимо:
- вскрывать корпус компьютера, не отключенного от электрической сети;
- использовать некачественные или изношенные провода, электрические розетки, удлинители и иные вспомогательные электрические аксессуары;
- располагать электрические провода таким образом, что на них можно наступить при ходьбе или случайно задеть телом при работе за компьютером.
Следует также знать, что на отдельных элементах компьютера (например, мониторах некоторых типов, источниках бесперебойного питания) высокое напряжение может сохраняться и некоторое время после отключения компьютера от сети.
Компьютер является и потенциальным источником пожарной опасности. Положенные на системный блок или источник питания листы бумаги, особенно если они закрывают вентиляционные отверстия, могут воспламениться (или привести к выходу из строя компьютера за счет перегрева). В вентиляционных отверстиях узлов компьютера неизбежно скапливается пыль, и это тоже не способствует его качественной работе. Эту пыль надо хотя бы раз в год удалять с помощью пылесоса (особенно из системного блока, не вскрывая его).
Давайте не будем путать: из того, что вы умеете программировать, инсталлировать и удалять программы, создавать презентации, общаться в Интернете и т. д., вовсе не следует, что вы являетесь квалифицированным специалистом по сборке-разборке компьютера. От правильной самооценки в этих вопросах зависит ваше здоровье (и даже жизнь).
Если правила техники безопасности при работе с компьютером, связанные с «электрической» составляющей, относительно просты и легко выполнимы, то правила личной гигиены в этой сфере (тоже не очень сложные) гораздо реже соблюдаются на практике, особенно когда мы не в школьном компьютерном классе, где за их соблюдением следит учитель, а дома. Вспомните, что элементарное требование «регулярно мойте руки мылом» предохраняет здоровье миллионов людей эффективнее самых совершенных лекарств, но многие люди болеют лишь потому, что его нарушили. При работе с компьютером имеет место аналогичная ситуация — люди, не соблюдая элементарные гигиенические нормы, теряют зрение, портят осанку, чрезмерно утомляются и даже доводят себя до психических расстройств. Длительная работа за компьютером негативно сказывается на многих функциях человеческого организма: эндокринной, иммунной и репродуктивной системах, на зрении и костно-мышечном аппарате.
Обсудим некоторые проблемы в этой сфере детальнее.
Электромагнитные излучения, сопровождающие работу системного блока, монитора и других узлов компьютера, традиционно рассматриваются как первостепенные источники опасности для человека. Несмотря на то что современные персональные компьютеры в этом отношении гораздо менее опасны, чем их прародители, эта угроза сохраняется. Современные жидкокристаллические мониторы практически не дают опасного излучения, в отличие от боковых и задних стенок системного блока, источников бесперебойного питания, и поэтому не следует ставить их вплотную к пользователю. В компьютерном классе, где стоит несколько компьютеров, системный блок соседнего компьютера не должен задней стенкой упираться в человека — на этот счет существуют строгие правила, как расставлять компьютеры.
Вредное влияние на зрение, оказываемое монитором, можно уменьшить как за счет высокого качества монитора, так и путем периодического выполнения несложных упражнений для глаз. Монитор должен удовлетворять международным стандартам безопасности, что фиксируется в сопроводительной документации. На него не должны падать блики от источников света; расстояние от экрана монитора до глаз пользователя должно составлять от 50 до 70 см. Не надо стремиться отодвинуть монитор как можно дальше, опасаясь вредных излучений, потому что для глаза важен также угол обзора наиболее характерных объектов. Оптимально размещение монитора на расстоянии примерно полутора размеров диагонали экрана. Важным параметром является частота кадров — она должна быть не менее 85 Гц. Периодически, почувствовав утомление зрения, необходимо сделать перерыв, отвести взгляд от экрана и сфокусировать его на удаленных предметах. Вредное влияние на зрение оказывает и недостаточная освещенность как помещения в целом, так и рабочего места в частности.
Вредное влияние на осанку, которое может привести к искривлению позвоночника и другим неприятностям, компенсируют правильным оснащением рабочего места — стола, стула, подставок для рук и ног. Рабочий стол и посадочное место должны иметь такую высоту, чтобы уровень глаз пользователя находился чуть выше центра монитора. Даже кратковременная работа с монитором, установленным слишком высоко, приводит к утомлению шейных отделов позвоночника. Клавиатура должна быть расположена на такой высоте, чтобы пальцы рук располагались на ней свободно, без напряжения. При работе с мышью рука не должна находиться на весу. Локоть руки или хотя бы запястье должны иметь твердую опору.
И наконец, нельзя не сказать о вредном влиянии на психику, наблюдаемом у некоторых пользователей персональных компьютеров, число которых, к сожалению, возрастает. Компьютерная зависимость, проявляющаяся в том, что люди (прежде всего молодые) теряют интерес ко всему, кроме компьютерных игр и/или общения в Интернете, по классификации Всемирной организации здравоохранения отнесена к опасным психическим расстройствам. Эти люди постепенно теряют связь с действительностью и начинают жить в воображаемом мире. «Техника безопасности» здесь состоит в самоконтроле и контроле со стороны окружающих, помогающих вовремя оторваться от виртуального мира и вернуться в мир реальный.
Закончим этот обзор на оптимистичной ноте. Компьютеры и информационные технологии стали одним из величайших приобретений человечества за всё время развития науки и техники. Увы, практически любое техническое приобретение имеет и негативные стороны, но при соблюдении определенных правил можно минимизировать вредные последствия, и они несопоставимы с теми возможностями, которые компьютерная техника дала человечеству.

|
5 |
| Глава 1. Информация |
11 |
§ 1.
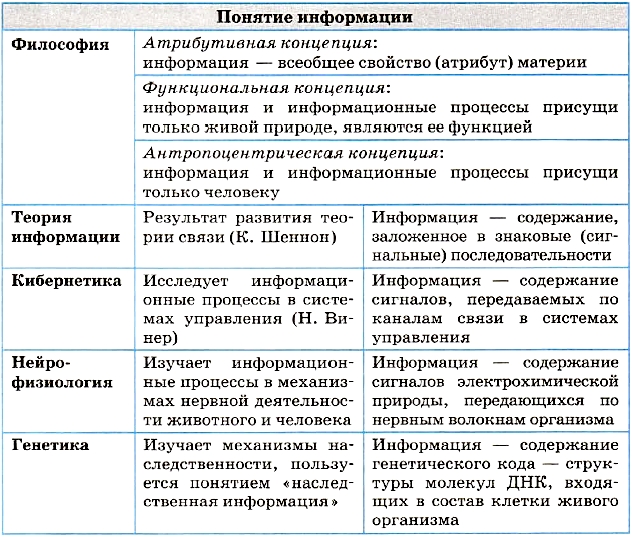
Понятие информации
§ 1. Понятие информации
Наверное, самый сложный вопрос в информатике — это «Что такое информация?». На него нет однозначного ответа. Смысл этого понятия зависит от контекста (содержания разговора, текста), в котором оно употребляется.
В курсе информатики основной школы информация рассматривалась в разных контекстах. С позиции человека, информация — это содержание сообщений, это самые разнообразные сведения, которые человек получает из окружающего мира через свои органы чувств. Из совокупности получаемой человеком информации формируются его знания об окружающем мире и о себе самом.
Рассказывая о компьютере, мы говорили, что компьютер — это универсальный программно управляемый автомат для работы с информацией. В таком контексте не обсуждается смысл информации. Смысл — это значение, которое придает информации человек. Компьютер же работает с битами, с двоичными кодами. Вникать в их «смысл» компьютер не в состоянии. Поэтому правильнее называть информацию, циркулирующую в устройствах компьютера, данными. Тем не менее в разговорной речи, в литературе часто говорят о том, что компьютер хранит, обрабатываем, передает и принимает информацию. Ничего страшного в этом нет. Надо лишь понимать, что в «компьютерном контексте» понятие «информация» отождествляется с понятием «данные».
В Толковом словаре В. И. Даля нет слова «информация». Термин «информация» начал широко употребляться с середины XX века.
В наибольшей степени понятие информации обязано своим распространением двум научным направлениям: теории связи и кибернетике. Автор теории связи Клод Шеннон, анализируя технические системы связи: телеграф, телефон, радио, рассматривал их как системы передачи информации. В таких системах информация передается в виде последовательностей сигналов: электрических или электромагнитных. Развитие теории связи послужило созданию теории информации, решающей проблему измерения информации.
Основатель кибернетики Норберт Винер анализировал разнообразные процессы управления в живых организмах и в технических системах. Процессы управления рассматриваются в кибернетике как информационные процессы. Информация в системах управления циркулирует в виде сигналов, передаваемых по информационным каналам.
В XX веке понятие информации повсеместно проникает в науку. Нейрофизиология (раздел биологии) изучает механизмы нервной деятельности животного и человека. Эта наука строит модель информационных процессов, происходящих в организме. Поступающая извне информация превращается в сигналы электрохимической природы, которые от органов чувств передаются по нервным волокнам к нейронам (нервным клеткам) мозга. Мозг передает управляющую информацию в виде сигналов той же природы к мышечным тканям, управляя, таким образом, органами движения. Описанный механизм хорошо согласуется с кибернетической моделью Н. Винера.
В другой биологической науке — генетике используется понятие наследственной информации, заложенной в структуре молекул ДНК, присутствующих в ядрах клеток живых организмов (растений, животных). Генетика доказала, что эта структура является своеобразным кодом, определяющим функционирование всего организма: его рост, развитие, патологии и пр. Через молекулы ДНК происходит передача наследственной информации от поколения к поколению.

Понятие информации относится к числу фундаментальных, т. е. является основополагающим для науки и не объясняется через другие понятия. В этом смысле информация встает в один ряд с такими фундаментальными научными понятиями, как вещество, энергия, пространство, время. Осмыслением информации как фундаментального понятия занимается наука философия.
Согласно одной из философских концепций, информация является свойством всего сущего, всех материальных объектов мира. Такая концепция информации называется атрибутивной (информация — атрибут всех материальных объектов). Информация в мире возникла вместе со Вселенной. С такой предельно широкой точки зрения, информация проявляется в воздействии одних объектов на другие, в изменениях, к которым такие воздействия приводят.
Другую философскую концепцию информации называют функциональной. Согласно функциональному подходу, информация появилась лишь с возникновением жизни, так как связана с функционированием сложных самоорганизующихся систем, к которым относятся живые организмы и человеческое общество. Можно еще сказать так: информация — это атрибут, свойственный только живой природе. Это один из существенных признаков, отделяющих в природе живое от неживого.
Третья философская концепция информации — антропоцентрическая, согласно которой информация существует лишь в человеческом сознании, в человеческом восприятии. Информационная деятельность присуща только человеку, происходит в социальных системах. Создавая информационную технику, человек создает инструменты для своей информационной деятельности.

Делая выбор между различными точками зрения, надо помнить, что всякая научная теория — лишь модель бесконечно сложного мира, поэтому она не может отражать его точно и в полной мере.
Можно сказать, что употребление понятия «информация» в повседневной жизни происходит в антропоцентрическом контексте. Для любого из нас естественно воспринимать информацию как сообщения, которыми обмениваются люди. Например, средства массовой информации (СМИ) предназначены для распространения сообщений, новостей среди населения.
Система основных понятий
Вопросы и задания
- Какие существуют основные философские концепции информации?
- Какая, с вашей точки зрения, концепция является наиболее верной?
- Благодаря развитию каких наук понятие информации стало широко употребляемым?
- В каких биологических науках активно используется понятие информации?
- Что такое наследственная информация?
- К какой философской концепции, на ваш взгляд, ближе употребление понятия информации в генетике?
- Если под информацией понимать только то, что распространяется через книги, рукописи, произведения искусства, средства массовой информации, то к какой философской концепции ее можно будет отнести?
- Согласны ли вы, что понятие информации имеет контекстный смысл? Если да, то покажите это на примерах.

Возможные ответы:
|
11 |
§ 2.
Предоставление информации, языки, кодирование
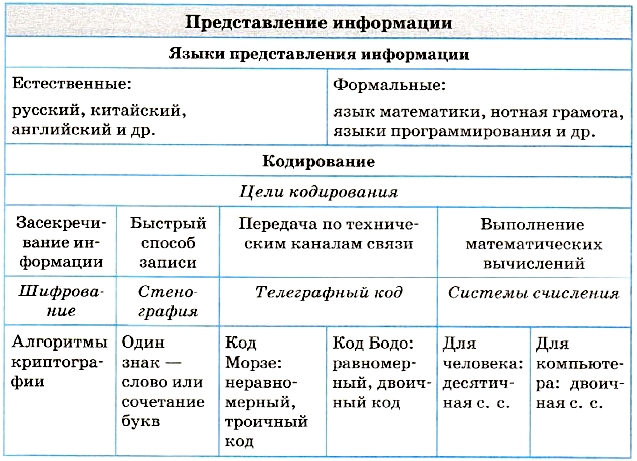
§ 2. Представление информации, языки, кодирование
Из курса основной школы вам известно:
- Историческое развитие человека, формирование человеческого общества связано с развитием речи, с появлением и распространением языков. Язык — это знаковая система для представления и передачи информации.
- Люди сохраняют свои знания в записях на различных носителях. Благодаря этому знания передаются не только в пространстве, но и во времени — от поколения к поколению.
- Языки бывают естественные, например русский, китайский, английский, и формальные, например математическая символика, нотная грамота, языки программирования.
Письменность и кодирование информации
Под словом «кодирование» понимают процесс представления информации, удобный для ее хранения и/или передачи. Следовательно, запись текста на естественном языке можно рассматривать как способ кодирования речи с помощью графических элементов (букв, иероглифов). Записанный текст является кодом, заключающим в себе содержание речи, т. е. информацию.
Процесс чтения текста — это обратный по отношению к письму процесс, при котором письменный текст преобразуется в устную речь. Чтение можно назвать декодированием письменного текста. Схематически эти два процесса изображены на рис. 1.1.

Рис. 1.1. Схема передачи информации с помощью письменности
Схема на рис. 1.1 типична для всех процессов, связанных с передачей информации.
Цели и способы кодирования
Теперь обратим внимание на то, что может существовать много способов кодирования одного и того же текста на одном и том же языке. Например, русский текст мы привыкли записывать с помощью русского алфавита. Но то же самое можно сделать, используя латинский алфавит. Иногда так приходится поступать, отправляя SMS по мобильному телефону, на котором нет русских букв, или электронное письмо на русском языке за границу, если у адресата нет русифицированного программного обеспечения. Например, фразу «Здравствуй, дорогой Саша!» приходится писать так: «Zdravstvui, dorogoi Sasha!».
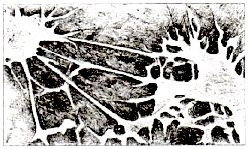
Существует множество способов кодирования. Например, стенография — быстрый способ записи устной речи. Стенография появилась во времена, когда не существовало техники звукозаписи. Ею владели лишь немногие специально обученные люди — стенографисты. Они успевали записывать текст синхронно с речью выступающего человека. В стенограмме один значок обозначает целое слово или сочетание букв. Расшифровать (декодировать) стенограмму мог только сам стенографист.
Посмотрите на текст стенограммы на рис. 1.2. Там написано следующее: «Говорить умеют все люди на свете. Даже у самых примитивных племен есть речь. Язык — это нечто всеобщее и самое человеческое, что есть на свете».
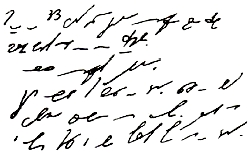
Рис. 1.2. Стенограмма
Можно придумать и другие способы кодирования.
Приведенные примеры иллюстрируют следующее важное правило: для кодирования одной и той же информации могут быть использованы разные способы; их выбор зависит от ряда обстоятельств: цели кодирования, условий, имеющихся средств. Если надо записать текст в темпе речи, делаем это с помощью стенографии; если надо передать текст за границу, пользуемся латинским алфавитом; если надо представить текст в виде, понятном для грамотного русского человека, записываем его по правилам грамматики русского языка.
Еще одно важное обстоятельство: выбор способа кодирования информации может быть связан с предполагаемым способом ее обработки. Обсудим это на примере представления чисел — количественной информации. Используя русский алфавит, можно записать число «тридцать пять». Используя же алфавит арабской десятичной системы счисления, пишем: 35. Пусть вам надо произвести вычисления. Скажите, какая запись удобнее для выполнения расчетов: «тридцать пять умножить на сто двадцать семь» или «35 х 127»? Очевидно, что для перемножения многозначных чисел вы будете пользоваться второй записью.
Заметим, что эти две записи, эквивалентные по смыслу, используют разные языки: первая — естественный русский язык, вторая — формальный язык математики, не имеющий национальной принадлежности. Переход от представления на естественном языке к представлению на формальном языке можно также рассматривать как кодирование. Человеку удобно использовать для кодирования чисел десятичную систему счисления, а компьютеру — двоичную систему.
Широко используемыми в информатике формальными языками являются языки программирования.
В некоторых случаях возникает потребность засекречивания текста сообщения или документа, для того чтобы его не смогли прочитать те, кому не положено. Это называется защитой от несанкционированного доступа. В таком случае секретный текст шифруется. В давние времена шифрование называлось тайнописью. Шифрование представляет собой процесс превращения открытого текста в зашифрованный, а дешифрование — процесс обратного преобразования, при котором восстанавливается исходный текст. Шифрование — это тоже кодирование, но с засекреченным методом, известным только источнику и адресату. Методами шифрования занимается наука криптография.
История технических способов кодирования информации
С появлением технических средств хранения и передачи информации возникли новые идеи и приемы кодирования. Первым техническим средством передачи информации на расстояние стал телеграф, изобретенный в 1837 году американцем Сэмюэлем Морзе (1791-1872). Телеграфное сообщение — это последовательность электрических сигналов, передаваемая от одного телеграфного аппарата по проводам к другому телеграфному аппарату. Эти технические обстоятельства привели Морзе к идее использования всего двух видов сигналов — короткого и длинного — для кодирования сообщения, передаваемого по линиям телеграфной связи.
Такой способ кодирования получил название азбуки Морзе. В ней каждая буква алфавита кодируется последовательностью коротких сигналов (точек) и длинных сигналов (тире). Буквы отделяются друг от друга паузами — отсутствием сигналов.
В таблице на рис. 1.3 показана азбука Морзе применительно к русскому алфавиту. Специальных знаков препинания в ней нет. Их обычно записывают словами: «тчк» — точка, «зпт» — запятая и т. п.
Самым знаменитым телеграфным сообщением является сигнал бедствия «SOS» (Save Our Souls — спасите наши души). Вот как он выглядит в коде азбуки Морзе:
• • • — — — • • •
Три точки обозначают букву S, три тире — букву О. Две паузы отделяют буквы друг от друга.

Рис. 1.3. Кодовая таблица азбуки Морзе
Характерной особенностью азбуки Морзе является переменная длина кода разных букв, поэтому код Морзе называют неравномерным кодом. Буквы, которые встречаются в тексте чаще, имеют более короткий код, чем редкие буквы. Например, код буквы «Е» — одна точка, а код буквы «Ъ» состоит из шести знаков. Зачем так сделано? Чтобы сократить длину всего сообщения. Но из-за переменной длины кода букв возникает проблема отделения букв друг от друга в тексте. Поэтому приходится для разделения использовать паузу (пропуск). Следовательно, телеграфный алфавит Морзе является троичным, так как в нем используется три знака: точка, тире, пропуск.
Равномерный телеграфный код был изобретен французом Жаном Морисом Бодо (1845-1903) в конце XIX века. В нем использовалось всего два вида сигналов. Неважно, как их назвать: точка и тире, плюс и минус, ноль и единица.
Это два отличающихся друг от друга электрических сигнала.
В коде Бодо длина кодов всех символов алфавита одинакова и равна пяти. В таком случае не возникает проблемы отделения букв друг от друга: каждая пятерка сигналов — это знак текста.
Код Бодо — это первый в истории техники способ двоичного кодирования информации. Благодаря идее Бодо удалось автоматизировать процесс передачи и печати букв. Был создан клавишный телеграфный аппарат. Нажатие клавиши с определенной буквой вырабатывает соответствующий пятиимпульсный сигнал, который передается по линии связи. Принимающий аппарат под воздействием этого сигнала печатает ту же букву на бумажной ленте.
Из курса информатики основной школы вам известно, что в современных компьютерах для кодирования текстов также применяется равномерный двоичный код. Проблемы кодирования информации в компьютере и при передаче данных по сети мы рассмотрим несколько позже.
Система основных понятий
Вопросы и задания
- Чем отличаются естественные языки от формальных?
- Как вы думаете, латынь — это естественный или формальный язык?
- С каким формальным языком программирования вы знакомы? Для чего он предназначен?
- Что такое кодирование и декодирование?
- От чего может зависеть способ кодирования?
- В чем преимущество кода Бодо по сравнению с кодом Морзе?
- В чем преимущество кода Морзе по сравнению с кодом Бодо?

Возможные ответы:
|
15 |
§
3.
Измерение информации. Алфавитный подход
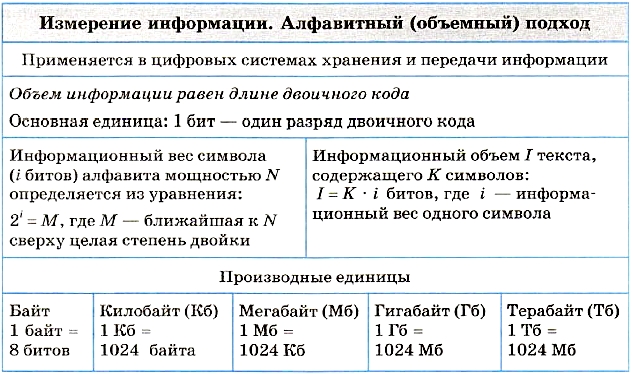
§ 3. Измерение информации. Алфавитный подход
Вопрос об измерении количества информации является очень важным как для науки, так и для практики. В самом деле, если информация является предметом нашей деятельности, мы ее храним, передаем, принимаем, обрабатываем. Поэтому важно договориться о способе ее измерения, позволяющем, например, ответить на вопросы: достаточно ли места на носителе, чтобы разместить нужную нам информацию, или сколько времени потребуется, чтобы передать ее по имеющемуся каналу связи. Величина, которая нас в этих ситуациях интересует, называется объемом информации. В таком случае говорят об алфавитном, или объемном, подходе к измерению информации.
Алфавитный подход к измерению информации применяется в цифровых (компьютерных) системах хранения и передачи информации. В этих системах используется двоичный способ кодирования информации. При алфавитном подходе для определения количества информации имеет значение лишь размер (объем) хранимого и передаваемого кода. Алфавитный подход еще называют объемным подходом. Из курса информатики 7-9 классов вы знаете, что если с помощью i-разрядного двоичного кода можно закодировать алфавит, состоящий из N символов (где N — целая степень двойки), то эти величины связаны между собой по формуле:
2i = N.
Число N называется мощностью алфавита.
Если, например, i = 2, то можно построить 4 двухразрядные комбинации из нулей и единиц, т. е. закодировать 4 символа. При i = 3 существует 8 трехразрядных комбинаций нулей и единиц (кодируется 8 символов):

Английский алфавит содержит 26 букв. Для записи текста нужны еще как минимум шесть символов: пробел, точка, запятая, вопросительный знак, восклицательный знак, тире. В сумме получается расширенный алфавит мощностью в 32 символа.
Поскольку 32 = 25, все символы можно закодировать всевозможными пятиразрядными двоичными кодами от 00000 до 11111. Именно пятиразрядный код использовался в телеграфных аппаратах, появившихся еще в XIX веке. Телеграфный аппарат при вводе переводил английский текст в двоичный код, длина которого в 5 раз больше, чем длина исходного текста.
|
В двоичном коде каждая двоичная цифра несет одну единицу информации, которая называется 1 бит.
|
|
Бит является основной единицей измерения информации.
|
Длина двоичного кода, с помощью которого кодируется символ алфавита, называется информационным весом символа. В рассмотренном выше примере информационный вес символа расширенного английского алфавита оказался равным 5 битам.
Информационный объем текста складывается из информационных весов всех составляющих текст символов. Например, английский текст из 1000 символов в телеграфном сообщении будет иметь информационный объем 5000 битов.
Алфавит русского языка включает 33 буквы. Если к нему добавить еще пробел и пять знаков препинания, то получится набор из 39 символов. Для двоичного кодирования символов такого алфавита пятиразрядного кода уже недостаточно. Нужен как минимум 6-разрядный код. Поскольку 26 = 64, остается еще резерв для 25 символов (64 - 39 = 25). Его можно использовать для кодирования цифр, всевозможных скобок, знаков математических операций и других символов, встречающихся в русском тексте. Следовательно, информационный вес символа в расширенном русском алфавите будет равен 6 битам. А текст из 1000 символов будет иметь объем 6000 битов.
Итак, если i — информационный вес символа алфавита, а К — количество символов в тексте, записанном с помощью этого алфавита, то информационный объем I текста выражается формулой:
I = К х i (битов).
Идея измерения количества информации в сообщении через длину двоичного кода этого сообщения принадлежит выдающемуся российскому математику Андрею Николаевичу Колмогорову (1903-1987). Согласно Колмогорову, количество информации, содержащееся в тексте, определяется минимально возможной длиной двоичного кода, необходимого для представления этого текста.
Для определения информационного веса символа полезно знать ряд целых степеней двойки. Вот как он выглядит в диапазоне от 21 до 210:

Поскольку мощность N алфавита может не являться целой степенью двойки, информационный вес символа алфавита мощности N определяется следующим образом. Находится ближайшее к N значение во второй строке таблицы, не меньшее чем N. Соответствующее значение i в первой строке будет равно информационному весу символа.
Пример. Определим информационный вес символа алфавита, включающего в себя все строчные и прописные русские буквы (66); цифры (10); знаки препинания, скобки, кавычки (10). Всего получается 86 символов.
Поскольку 26 < 86 < 27, информационный вес символов данного алфавита равен 7 битам. Это означает, что все 86 символов можно закодировать семиразрядными двоичными кодами.
Для двоичного представления текстов в компьютере чаще всего применяется восьмиразрядный код. С помощью восьмиразрядного кода можно закодировать алфавит из 256 символов, поскольку 256 = 28. В стандартную кодовую таблицу (например, используемую в ОС Windows таблицу ANSI) помещаются все необходимые символы: английские и русские буквы — прописные и строчные, цифры, знаки препинания, знаки арифметических операций, всевозможные скобки и пр.
Более крупной, чем бит, единицей измерения информации является байт: 1 байт = 8 битов.
|
Информационный объем текста в памяти компьютера измеряется в байтах. Он равен количеству символов в записи текста.
|
Одна страница текста на листе формата А4 кегля 12 с одинарным интервалом между строками в компьютерном представлении будет иметь объем 4000 байтов, так как на ней помещается примерно 4000 знаков.
Помимо бита и байта, для измерения информации используются и более крупные единицы:
1 Кб (килобайт) = 210 байтов = 1024 байта;
1 Мб (мегабайт) = 210 Кб = 1024 Кб;
1 Гб (гигабайт) = 210 Мб = 1024 Мб;
1 Тб (терабайт) = 210 Гб = 1024 Гб.
Объем той же страницы текста будет равен приблизительно 3,9 Кб. А книга из 500 таких страниц займет в памяти компьютера примерно 1,9 Мб.
В компьютере любые виды информации: тексты, числа, изображения, звуки — представляются в форме двоичного кода.
|
Объем информации любого вида, выраженный в битах, равен длине двоичного кода, в котором эта информация представлена.
|
Система основных понятий
Вопросы и задания
- Есть ли связь между алфавитным подходом к измерению информации и содержанием информации?
- В чем можно измерить объем письменного или печатного текста?
- Оцените объем одной страницы данного учебника в байтах.
- Что такое бит с позиции алфавитного подхода к измерению информации?
- Как определяется информационный объем текста по А. Н. Колмогорову?
- Какой информационный вес имеет каждая буква русского алфавита?
- Какие единицы используются для измерения объема информации на компьютерных носителях?
- Сообщение, записанное буквами из 64-символьного алфавита, содержит 100 символов. Какой объем информации оно несет?
- Сколько символов содержит сообщение, записанное с помощью 16-символьного алфавита, если его объем составляет 1/16 Мб?
- Сообщение занимает 2 страницы и содержит 1/16 Кб информации. На каждой странице 256 символов. Какова мощность используемого алфавита?
- Возьмите страницу текста из данного учебника и подсчитайте информационные объемы текста, получаемые при кодировании его семиразрядным и восьмиразрядным кодами. Результаты выразите в килобайтах и мегабайтах.

Возможные ответы:
|
21 |
§
4.
Измерение информации. Содержательный подход
§ 4. Измерение информации. Содержательный подход
Неопределенность знания и количество информации
Содержательный подход к измерению информации отталкивается от определения информации как содержания сообщения, получаемого человеком. Сущность содержательного подхода заключается в следующем: сообщение, информирующее об исходе како-го-то события, снимает неопределенность знания человека об этом событии.
Чем больше первоначальная неопределенность знания, тем больше информации несет сообщение, снимающее эту неопределенность.
Приведем примеры, иллюстрирующие данное утверждение.
Ситуация 1. В ваш класс назначен новый учитель информатики; на вопрос «Это мужчина или женщина?» вам ответили: «Мужчина».
Ситуация 2. На чемпионате страны по футболу играли команды «Динамо» и «Зенит». Из спортивных новостей по радио вы узнаете, что игра закончилась победой «Зенита».
Ситуация 3. На выборах мэра города было представлено четыре кандидата. После подведения итогов голосования вы узнали, что избран Н. Н. Никитин.
Вопрос: в какой из трех ситуаций полученное сообщение несет больше информации?
Неопределенность знания — это количество возможных вариантов ответа на интересовавший вас вопрос. Еще можно сказать: возможных исходов события. Здесь событие — например, выборы мэра; исход — выбор, например, Н. Н. Никитина.
В первой ситуации 2 варианта ответа: мужчина, женщина; во второй ситуации 3 варианта: выиграл «Зенит», ничья, выиграло «Динамо»; в третьей ситуации — 4 варианта: 4 кандидата на пост мэра.
Согласно данному выше определению, наибольшее количество информации несет сообщение в третьей ситуации, поскольку неопределенность знания об исходе события в этом случае была наибольшей.
В 40-х годах XX века проблема измерения информации была решена американским ученым Клодом Шенноном (1916-2001) — основателем теории информации. Согласно Шеннону, информация — это снятая неопределенность знания человека об исходе какого-то события.
В теории информации единица измерения информации определяется следующим образом.
|
Сообщение, уменьшающее неопределенность знания об исходе некоторого события в два раза, несет 1 бит информации.
|
Согласно этому определению, сообщение в первой из описанных ситуаций несет 1 бит информации, поскольку из двух возможных вариантов ответа был выбран один.
Следовательно, количество информации, полученное во второй и в третьей ситуациях, больше, чем один бит. Но как измерить это количество?
Рассмотрим еще один пример.
Ученик написал контрольную по информатике и спрашивает учителя о полученной оценке. Оценка может оказаться любой: от 2 до 5. На что учитель отвечает: «Угадай оценку за два вопроса, ответом на которые может быть только "да" или "нет"». Подумав, ученик задал первый вопрос: «Оценка выше тройки?». «Да», — ответил учитель. Второй вопрос: «Это пятерка?». «Нет», — ответил учитель. Ученик понял, что он получил четверку. Какая бы ни была оценка, таким способом она будет угадана!
Первоначально неопределенность знания (количество возможных оценок) была равна четырем. С ответом на каждый вопрос неопределенность знания уменьшалась в 2 раза и, следовательно, согласно данному выше определению, передавался 1 бит информации.

Узнав оценку (одну из четырех возможных), ученик получил 2 бита информации.
Рассмотрим еще один частный пример, а затем выведем общее правило.
Вы едете на электропоезде, в котором 8 вагонов, а на вокзале вас встречает товарищ. Товарищ позвонил вам по мобильному телефону и спросил, в каком вагоне вы едете. Вы предлагаете угадать номер вагона, задав наименьшее количество вопросов, ответами на которые могут быть только слова «да» или «нет».
Немного подумав, товарищ стал спрашивать:
— Номер вагона больше четырех?
— Да.
— Номер вагона больше шести?
— Нет.
— Это шестой вагон?
— Нет.
— Ну теперь все ясно! Ты едешь в пятом вагоне!
Схематически поиск номера вагона выглядит так:
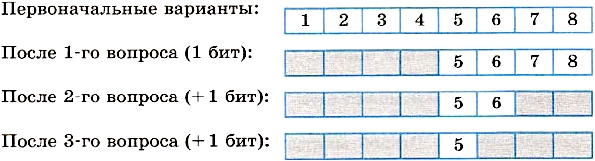
Каждый ответ уменьшал неопределенность знания в два раза. Всего было задано три вопроса. Значит, в сумме набрано 3 бита информации. То есть сообщение о том, что вы едете в пятом вагоне, несет 3 бита информации.
Способ решения проблемы, примененный в примерах с оценками и вагонами, называется методом половинного деления: ответ на каждый вопрос уменьшает неопределенность знания, имеющуюся перед ответом на этот вопрос, наполовину. Каждый такой ответ несет 1 бит информации.
Заметим, что решение подобных проблем методом половинного деления наиболее рационально. Таким способом всегда можно угадать, например, любой из восьми вариантов за 3 вопроса. Если бы поиск производился последовательным перебором: «Ты едешь в первом вагоне?» «Нет», «Во втором вагоне?» «Нет» и т. д., то про пятый вагон вы смогли бы узнать после пяти вопросов, а про восьмой — после восьми.
«Главная формула» информатики
Сформулируем одно очень важное условие, относящееся к рассмотренным примерам. Во всех ситуациях предполагается, что все возможные исходы события равновероятны. Равновероятно, что учитель может быть мужчиной или женщиной; равновероятен любой исход футбольного матча, равновероятен выбор одного из четырех кандидатов в мэры города. То же относится и к примерам с оценками и вагонами.
Тогда полученные нами результаты описываются следующими формулировками:
- сообщение об одном из двух равновероятных исходов некоторого события несет 1 бит информации;
- сообщение об одном из четырех равновероятных исходов некоторого события несет 2 бита информации;
- сообщение об одном из восьми равновероятных исходов некоторого события несет 3 бита информации.
Обозначим буквой N количество возможных исходов события, или, как мы это еще называли, — неопределенность знания. Буквой i будем обозначать количество информации в сообщении об одном из N результатов.
В примере с учителем: N = 2, i = 1 бит;
в примере с оценками: N = 4, i = 2 бита;
в примере с вагонами: N = 8, i = 3 бита.
Нетрудно заметить, что связь между этими величинами выражается следующей формулой:
2i = N.
Действительно: 21 = 2 ; 22 = 4 ; 23 = 8.
С полученной формулой вы уже знакомы из курса информатики для 7 класса и еще не однажды с ней встретитесь. Значение этой формулы столь велико, что мы назвали ее главной формулой информатики. Если величина N известна, a i неизвестно, то данная формула становится уравнением для определения i. В математике такое уравнение называется показательным уравнением.
Пример. Вернемся к рассмотренному выше примеру с вагонами. Пусть в поезде не 8, а 16 вагонов. Чтобы ответить на вопрос, какое количество информации содержится в сообщении о номере искомого вагона, нужно решить уравнение:
2i = 16.
Поскольку 16 = 24 , то i = 4 бита.
|
Количество информации i, содержащееся в сообщении об одном из N равновероятных исходов некоторого события, определяется из решения показательного уравнения:
2i = N.
|
Пример. В кинозале 16 рядов, в каждом ряду 32 места. Какое количество информации несет сообщение о том, что вам купили билет на 12-й ряд, 10-е место?
Решение задачи: в кинозале всего 16 • 32 = 512 мест. Сообщение о купленном билете однозначно определяет выбор одного из этих мест. Из уравнения 2i = 512 = 29 получаем: i = 9 битов.
Но эту же задачу можно решать иначе. Сообщение о номере ряда несет 4 бита информации, так как 24 = 16. Сообщение о номере места несет 5 битов информации, так как 25 = 32. В целом сообщение про ряд и место несет: 4 + 5 = 9 битов информации.
Данный пример иллюстрирует выполнение закона аддитивности количества информации (правило сложения): количество информации в сообщении одновременно о нескольких результатах независимых друг от друга событий равно сумме количеств информации о каждом событии отдельно.
Сделаем одно важное замечание. С формулой 2i = N мы уже встречались, обсуждая алфавитный подход к измерению информации (см. § 3). В этом случае N рассматривалось как мощность алфавита, a i — как информационный вес каждого символа алфавита. Если допустить, что все символы алфавита появляются в тексте с одинаковой частотой, т. е. равновероятно, то информационный вес символа i тождественен количеству информации в сообщении о появлении любого символа в тексте. При этом N — неопределенность знания о том, какой именно символ алфавита должен стоять в данной позиции текста. Данный факт демонстрирует связь между алфавитным и содержательным подходами к измерению информации.
Формула Хартли
Если значение N равно целой степени двойки (4, 8, 16, 32, 64 и т. д.), то показательное уравнение легко решить в уме, поскольку i будет целым числом. А чему равно количество информации в сообщении о результате матча «Динамо»-«Зенит»? В этой ситуации N = 3. Можно догадаться, что решение уравнения
2i = 3
будет дробным числом, лежащим между 1 и 2, поскольку 21 = 2 < 3, а 22 = 4 > 3. А как точнее узнать это число?
В математике существует функция, с помощью которой решается показательное уравнение. Эта функция называется логарифмом, и решение нашего уравнения записывается следующим образом:
i = log2N.
Читается это так: «логарифм от N по основанию 2». Смысл очень простой: логарифм по основанию 2 от N — это степень, в которую нужно возвести 2, чтобы получить N. Например, вычисление уже известных вам значений можно представить так:
log22 = 1, log24 = 2, log28 = 3.
Значения логарифмов находятся с помощью специальных логарифмических таблиц. Также можно использовать инженерный калькулятор или табличный процессор. Определим количество информации, полученной из сообщения об одном исходе события из трех равновероятных, с помощью электронной таблицы. На рисунке 1.4 представлены два режима электронной таблицы: режим отображения формул и режим отображения значений.

Рис. 1.4. Определение количества информации в электронных таблицах с помощью функции логарифма
В табличном процессоре Microsoft Excel функция логарифма имеет следующий вид: LOG(apryмент; основание). Аргумент — значение N находится в ячейке А2, а основание логарифма равно 2. В результате получаем с точностью до девяти знаков после запятой:
i = log23 = 1,584962501 (бита).
Формула для измерения количества информации: i = log2N была предложена американским ученым Ральфом Хартли (1888-1970) — одним из основоположников теории информации.
|
Формула Хартли:
i = log2N = log2N
Здесь i — количество информации, содержащееся в сообщении об одном из N равновероятных исходов события.
|
Данный пример показал, что количество информации, определяемое с использованием содержательного подхода, может быть дробной величиной, в то время как информационный объем, вычисляемый путем применения алфавитного подхода, может иметь только целочисленное значение.
Система основных понятий

Вопросы и задания
- Что такое неопределенность знания об исходе некоторого события?
- Как определяется единица измерения количества информации в рамках содержательного подхода?
- Придумайте несколько ситуаций, при которых сообщение несет 1 бит информации.
- В каких случаях и по какой формуле можно вычислить количество информации, содержащейся в сообщении, используя содержательный подход?
- Сколько битов информации несет сообщение о том, что из колоды в 32 карты достали «даму пик»?
- При угадывании методом половинного деления целого числа из диапазона от 1 до N был получен 1 байт информации. Чему равно N?
- Проводятся две лотереи: «4 из 32» и «5 из 64». Сообщение о результатах какой из лотерей несет больше информации?
- Используя формулу Хартли и электронные таблицы, определите количество информации в сообщениях о равновероятных событиях:
а) на шестигранном игральном кубике выпала цифра 3;
б) в следующем году ремонт в школе начнется в феврале;
в) я приобрел абонемент в бассейн на среду;
г) из 30 учеников класса дежурить в школьной столовой назначили Дениса Скворцова.
- Используя закон аддитивности количества информации, решите задачу о билете в кинотеатр со следующим дополнительным условием: в кинотеатре 4 зала. В билете указан номер зала, номер ряда и номер места. Какое количество информации заключено в билете?

Возможные ответы:
|
26 |
§
5.
Представление чисел в компьютере
§ 5. Представление чисел в компьютере
Главные правила представления данных в компьютере
Если бы мы могли заглянуть в содержание компьютерной памяти, то увидели бы там примерно то, что условно изображено на рис. 1.5.

Рис. 1.5. Образ компьютерной памяти
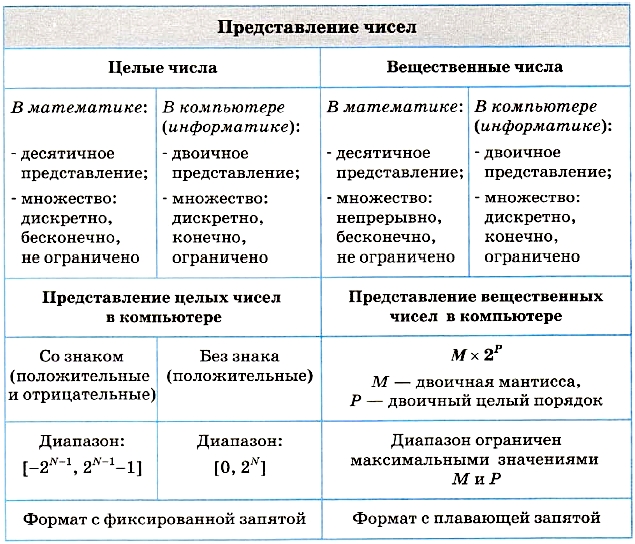
Рисунок 1.5 отражает известное вам еще из курса информатики основной школы правило представления данных, которое назовем правилом № 1: данные (и программы) в памяти компьютера хранятся в двоичном виде, т. е. в виде цепочек единиц и нулей.
Современный компьютер может хранить и обрабатывать данные, представляющие информацию четырех видов: числовую, текстовую, графическую, звуковую. Двоичный код, изображенный на рис. 1.5, может относиться к любому виду данных.
Правило № 2: представление данных в компьютере дискретно.
Правило № 3: множество представимых в памяти компьютера величин ограничено и конечно.
Представление чисел
Сначала поясним на образном примере, что такое дискретность.
Дискретное множество состоит из отделенных друг от друга элементов. Например, песок дискретен, поскольку он состоит из отдельных песчинок. А вода или масло непрерывны (в рамках наших ощущений, поскольку отдельные молекулы мы всё равно ощутить не можем). Этот пример нужен нам только для аналогии. Здесь мы не станем углубляться в изучение материального мира, а вернемся к предмету изучения информатики — информации.
Самым традиционным видом данных, с которым работают компьютеры, являются числа. ЭВМ первого поколения умели решать только математические задачи. Люди начали работать с числами еще с первобытных времен. Первоначально человек оперировал лишь целыми положительными (натуральными) числами: 1, 2, 3, 4, ... . Очевидно, что натуральный ряд — это дискретное множество чисел.
В математике ряд натуральных чисел бесконечен и не ограничен. С появлением в математике понятия отрицательного числа (Р. Декарт, XVII век в Европе; в Индии значительно раньше) оказалось, что множество целых чисел не ограничено как «справа», так и «слева». Покажем это на числовой оси (рис. 1.6), символы оо обозначают бесконечность.
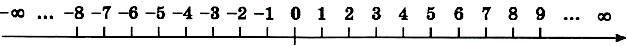
Рис. 1.6. Математическое множество целых чисел на числовой оси
Из сказанного следует вывод: множество целых чисел в математике дискретно и не ограничено. Отметим еще один факт: разность соседних чисел натурального ряда (данного и предыдущего) всегда равна единице. Эту величину назовем шагом числовой последовательности.
Любое вычислительное устройство (компьютер, калькулятор) может работать только с ограниченным множеством целых чисел. Возьмите в руки калькулятор, на индикаторном табло которого помещается 10 знаков. Самое большое положительное число, которое на него поместится:

Самое большое по абсолютной величине (модулю)

Аналогично дело обстоит и в компьютере.
Целые числа в компьютере
Правило № 4: в памяти компьютера числа хранятся в двоичной системе счисления*. С двоичной системой счисления вы знакомы из курса информатики 7-9 классов. Например, если под целое число выделяется ячейка памяти размером в 16 битов, то самое большое целое положительное число будет таким:

В десятичной системе счисления оно равно:
215 - 1 = 32 767.
Здесь первый бит играет роль знака числа. Ноль — признак положительного числа. Самое большое по модулю отрицательное число равно -32 768. Напомним (это было в курсе информатики основной школы), как получить его внутреннее представление:
- перевести число 32 768 в двоичную систему счисления; это легко, поскольку 32768 = 215:
1000000000000000;
- инвертировать этот двоичный код, т. е. заменить нули на единицы, а единицы — на нули:
0111111111111111;
- прибавить единицу к этому двоичному числу (складывать надо по правилам двоичной арифметики), в результате получим:

Единица в первом бите обозначает знак «минус». Не нужно думать, что полученный код — это «минус ноль». Этот код представляет число -32 768. Таковы правила машинного представления целых чисел. Данное представление называется дополнительным кодом.
Если под целое число в памяти компьютера отводится N битов, то диапазон значений целых чисел:
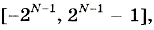
то есть ограниченность целого числа в компьютере возникает из-за ограничений на размер ячейки памяти. Отсюда же следует и конечность множества целых чисел.
Мы рассмотрели формат представления целых чисел со знаком, т. е. положительных и отрицательных. Бывает, что нужно работать только с положительными целыми числами. В таком случае используется формат представления целых чисел без знака. В этом формате самое маленькое число — ноль (все биты — нули), а самое большое число для 16-разрядной ячейки:

В десятичной системе это 216 - 1 = 65 535, примерно в два раза больше по модулю, чем в представлении со знаком.
Из всего сказанного делаем вывод: целые числа в памяти компьютера — это дискретное, ограниченное и конечное множество.
Границы множества целых чисел зависят от размера выделяемой ячейки памяти под целое число, а также от формата: со знаком или без знака. Шаг в компьютерном представлении последовательности целых чисел, как и в математическом, остается равным единице.
Рисунок 1.7 отражает то обстоятельство, что при переходе от математического представления множества целых чисел к представлению, используемому в информатике (компьютере), происходит переход к ограниченности и конечности.
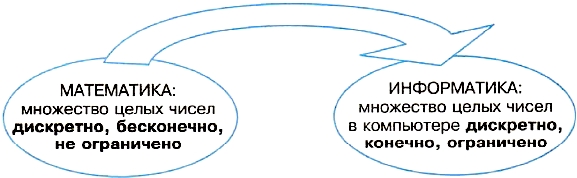
Рис. 1.7. Представление о множестве целых чисел в математике и в информатике
Вещественные числа в компьютере
Понятие вещественного (действительного) числа в математику ввел Исаак Ньютон в XVIII веке. В математике множество вещественных чисел непрерывно, бесконечно и не ограничено. Оно включает в себя множество целых чисел и еще бесконечное множество нецелых чисел. Между двумя любыми точками на числовой оси лежит бесконечное множество вещественных чисел, что и означает непрерывность множества.
Как мы говорили выше, числа в компьютере (в том числе и вещественные) представлены в двоичной системе счисления. Покажем, что множество вещественных чисел в компьютере дискретно, ограничено и конечно. Нетрудно догадаться, что это, так же как и в случае целых чисел, вытекает из ограничения размера ячейки памяти.
Снова для примера возьмем калькулятор с десятиразрядным индикаторным табло. Экспериментально докажем дискретность представления вещественных чисел. Выполним на калькуляторе деление 1 на 3. Из математики вам известно, что 1/3 — это рациональная дробь, представление которой в виде десятичной дроби содержит бесконечное количество цифр: 0,3333333333... (3 в периоде). На табло калькулятора вы увидите:

Первый разряд зарезервирован под знак числа. После запятой сохраняется 8 цифр, а остальные не вмещаются в разрядную сетку (так это обычно называют). Значит, это не точное значение, равное 1/3, а его «урезанное» значение.
Следующее по величине число, которое помещается в разрядную сетку:

Оно больше предыдущего на 0,00000001. Это шаг числовой последовательности. Следовательно, два рассмотренных числа разделены между собой конечным отрезком. Очевидно, что предыдущее число такое:

Оно тоже отделено от своего «соседа справа» по числовой оси шагом 0,00000001. Отсюда делаем вывод: множество вещественных чисел, представимых в калькуляторе, дискретно, поскольку числа отделены друг от друга конечными отрезками.
А теперь выясним вот что: будет ли шаг в последовательности вещественных чисел на калькуляторе постоянной величиной (как у целых чисел)?
Вычислим выражение 100000/3. Получим:

Это число в 100 000 раз больше предыдущего и, очевидно, тоже приближенное. Легко понять, что следующее вещественное число, которое можно получить на табло калькулятора, будет больше данного на 0,0001. Шаг стал гораздо больше.
Отсюда приходим к выводу: множество вещественных чисел, представимых в калькуляторе, дискретно с переменной величиной шага между соседними числами.
Если отметить на числовой оси точные значения вещественных чисел, которые представимы в калькуляторе, то эти точки будут расположены вдоль оси неравномерно. Ближе к нулю — чаще, дальше от нуля — реже (рис. 1.8).

Рис. 1.8. Условное представление взаимного расположения множества вещественных чисел, представимых в компьютере
Все выводы, которые мы делаем на примере калькулятора, полностью переносятся на компьютер с переходом к двоичной системе счисления и с учетом размера ячейки компьютера, отводимой под вещественные числа. Неравномерное расположение вещественных чисел, представимых в компьютере, также имеет место.
Ответим на вопрос: ограничено ли множество вещественных чисел в памяти компьютера? Если продолжать эксперименты с калькулятором, то ответ на этот вопрос будет таким: да, мнолсест-во вещественных чисел в калькуляторе ограничено. Причиной тому служит все та же ограниченность разрядной сетки. Отсюда же следует и конечность множества.
Самое большое число у разных калькуляторов может оказаться разным. У самого простого это будет то же число, что мы получали раньше: 999999999. Если прибавить к нему единицу, то калькулятор выдаст сообщение об ошибке. А на другом, более «умном» и дорогом, калькуляторе прибавление единицы приведет к такому результату:

Данную запись на табло надо понимать так: 1 • 109.
Такой формат записи числа называется форматом с плавающей запятой, в отличие от всех предыдущих примеров, где рассматривалось представление чисел в формате с фиксированной запятой.
Число, стоящее перед буквой «е», называется мантиссой, а стоящее после — порядком. «Умный» калькулятор перешел к представлению чисел в формате с плавающей запятой после того, как под формат с фиксированной запятой не стало хватать места на табло.
В компьютере то же самое: числа могут представляться как в формате с фиксированной запятой (обычно это целые числа), так и в формате с плавающей запятой.
Но и для формата с плавающей запятой тоже есть максимальное число. В нашем «подопытном» калькуляторе это число:

То есть 99999 • 1099. Самое большое по модулю отрицательное значение -99999 • 1099. Данные числа являются целыми, но именно они ограничивают представление любых чисел (целых и вещественных) в калькуляторе.
В компьютере всё организовано аналогично, но предельные значения еще больше. Это зависит от разрядности ячейки памяти, выделяемой под число, и от того, сколько разрядов выделяется под порядок и под мантиссу.
Рассмотрим пример: пусть под всё число в компьютере выделяется 8 байтов — 64 бита, из них под порядок — 2 байта, под мантиссу — 6 байтов. Тогда диапазон вещественных чисел, в переводе в десятичную систему счисления, оказывается следующим:
±(5 • 10-324 - 1,7 • 10308).
Завершая тему, посмотрим на рис. 1.9. Смысл, заложенный в нем, такой: непрерывное, бесконечное и не ограниченное множество вещественных чисел, которое рассматривает математика, при его представлении в компьютере обращается в дискретное, конечное и ограниченное множество.
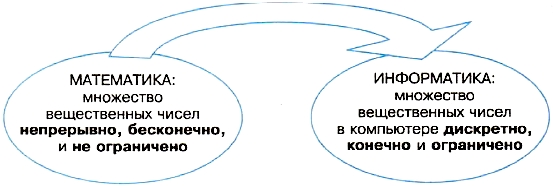
Рис. 1.9. Представление о множестве вещественных чисел в математике и в информатике
Система основных понятий
Вопросы и задания
- Почему множество целых чисел, представимых в памяти компьютера, дискретно, конечно и ограничено?
- Определите диапазон целых чисел, хранящихся в 1 байте памяти в двух вариантах: со знаком и без знака.
- Получите внутреннее представление числа 157 в 8-разрядной ячейке памяти в формате со знаком.
- Получите внутреннее представление числа -157 в 8-разрядной ячейке памяти в формате со знаком.
- Почему множество действительных (вещественных) чисел, представимых в памяти компьютера, дискретно, конечно и ограничено?
- На какие две части делится число в формате с плавающей запятой?
* Конечно, и «внутри калькулятора» числа представляются в двоичном виде. Однако мы в это вдаваться не будем, рассмотрев лишь внешнее представление. Пример с калькулятором нам нужен был только для иллюстрации проблемы ограниченности.

Возможные ответы:
|
34 |
§
6.
Представление текста, изображения и звука в компьютере
§ 6. Представление текста, изображения и звука в компьютере
В этом параграфе обсудим способы компьютерного кодирования текстовой, графической и звуковой информации. С текстовой и графической информацией конструкторы «научили» работать ЭВМ, начиная с третьего поколения (1970-е годы). А работу со звуком «освоили» лишь машины четвертого поколения, современные персональные компьютеры. С этого момента началось распространение технологии мультимедиа.
Что принципиально нового появлялось в устройстве компьютеров с освоением ими новых видов информации? Главным образом, это периферийные устройства для ввода и вывода текстов, графики, видео, звука. Процессор же и оперативная память по своим функциям изменились мало. Существенно возросло их быстродействие, объем памяти. Но как это было на первых поколениях ЭВМ, так и осталось на современных ПК — основным навыком процессора в обработке данных является умение выполнять вычисления с двоичными числами. Обработка текста, графики и звука представляет собой тоже обработку числовых данных. Если сказать еще точнее, то это обработка целых чисел. По этой причине компьютерные технологии называют цифровыми технологиями.
О том, как текст, графика и звук сводятся к целым числам, будет рассказано дальше. Предварительно отметим, что здесь мы снова встретимся с главной формулой информатики:
2i = N.
Смысл входящих в нее величин здесь следующий: i — разрядность ячейки памяти (в битах), N — количество различных целых положительных чисел, которые можно записать в эту ячейку.
Текстовая информация
Принципиально важно, что текстовая информация уже дискретна — состоит из отдельных знаков. Поэтому возникает лишь технический вопрос — как разместить ее в памяти компьютера.
Напомним о байтовом принципе организации памяти компьютеров, обсуждавшемся в курсе информатики основной школы. Вернемся к рис. 1.5. Каждая клеточка на нем обозначает бит памяти. Восемь подряд расположенных битов образуют байт памяти. Байты пронумерованы. Порядковый номер байта определяет его адрес в памяти компьютера. Именно по адресам процессор обращается к данным, читая или записывая их в память (рис. 1.10).

Рис. 1.10. Байтовая организация памяти
Модель представления текста в памяти весьма проста. За каждой буквой алфавита, цифрой, знаком препинания и иным общепринятым при записи текста символом закрепляется определенный двоичный код, длина которого фиксирована. В популярных системах кодировки (Windows-1251, КОI8 и др.) каждый символ заменяется на 8-разрядное целое положительное двоичное число; оно хранится в одном байте памяти. Это число является порядковым номером символа в кодовой таблице. Согласно главной формуле информатики, определяем, что размер алфавита, который можно закодировать, равен: 28 = 256. Этого количества вполне достаточно для размещения двух алфавитов естественных языков (английского и русского) и всех необходимых дополнительных символов.
Поскольку в мире много языков и много алфавитов, постепенно совершается переход на международную систему кодировки Unicode, в которой используются многобайтовые коды. Например, если код символа занимает 2 байта, то с его помощью можно закодировать 216 = 65 536 различных символов.
При работе с электронной почтой почтовая программа иногда нас спрашивает, не хотим ли мы прибегнуть к кодировке Unicode для пересылаемых сообщений. Таким способом можно избежать проблемы несоответствия кодировок, из-за которой иногда не удается прочитать русский текст.
Текстовый документ, хранящийся в памяти компьютера, состоит не только из кодов символьного алфавита. В нем также содержатся коды, управляющие форматами текста при его отображении на мониторе или на печати: тип и размер шрифта, положение строк, поля и отступы и пр. Кроме того, текстовые процессоры (например, Microsoft Word) позволяют включать в документ и редактировать такие «нелинейные» объекты, как таблицы, оглавления, ссылки и гиперссылки, историю вносимых изменений и т. д. Всё это также представляется в виде последовательности байтовых кодов.
Графическая информация
Из курса информатики 7-9 классов вы знакомы с общими принципами компьютерной графики, с графическими технологиями. Здесь мы немного подробнее, чем это делалось раньше, рассмотрим способы представления графических изображений в памяти компьютера.
Принцип дискретности компьютерных данных справедлив и для графики. Здесь можно говорить о дискретном представлении изображения {рисунка, фотографии, видеокадров) и дискретности цвета.
Дискретное представление изображения. Изображение на экране монитора дискретно. Оно составляется из отдельных точек, которые называются пикселями (picture elements — элементы рисунка). Это связано с техническими особенностями устройства экрана, независимо от его физической реализации, будь то монитор на электронно-лучевой трубке, жидкокристаллический или плазменный. Эти «точки» столь близки друг другу, что глаз не различает промежутков между ними, поэтому изображение воспринимается как непрерывное, сплошное. Если выводимое из компьютера изображение формируется на бумаге (принтером или плоттером), то линии на нем также выглядят непрерывными. Однако в основе всё равно лежит печать близких друг к другу точек.
В зависимости от того, на какое графическое разрешение экрана настроена операционная система компьютера, на нем могут размещаться изображения, имеющие размер 800 х 600, 1024 х 768 и более пикселей. Такая прямоугольная матрица пикселей на экране компьютера называется растром.
Качество изображения зависит не только от размера растра, но и от размера экрана монитора, который обычно характеризуется длиной диагонали. Существует параметр разрешения экрана. Этот параметр измеряется в точках на дюйм (по-английски dots per inch — dpi). У монитора с диагональю 15 дюймов размер изображения на экране составляет примерно 28 х 21 см2. Зная, что в одном дюйме 25,4 мм, можно рассчитать, что при работе монитора в режиме 800 х 600 пикселей разрешение экранного изображения равно 72 dpi.
При печати на бумаге разрешение должно быть намного выше. Полиграфическая печать полноцветного изображения требует разрешения 200-300 dpi. Стандартный фотоснимок размером 10 х 15 см2 должен содержать примерно 1000 х 1500 пикселей.
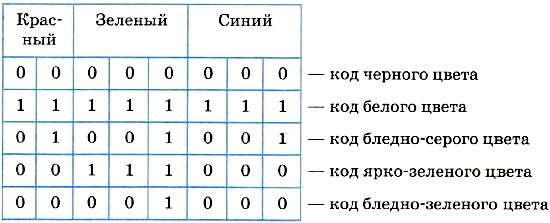
Дискретное представление цвета. Восстановим ваши знания о кодировании цвета, полученные из курса информатики основной школы. Основное правило звучит так: любой цвет точки на экране компьютера получается путем смешивания трех базовых цветов: красного, зеленого, синего. Этот принцип называется цветовой моделью RGB (Red, Green, Blue).
Двоичный код цвета определяет, в каком соотношении находятся интенсивности трех базовых цветов. Если все они смешиваются в одинаковых долях, то в итоге получается белый цвет. Если все три компоненты «выключены», то цвет пикселя — черный. Все остальные цвета лежат между белым и черным.
Дискретность цвета состоит в том, что интенсивности базовых цветов могут принимать конечное число дискретных значений.
Пусть, например, размер кода цвета пикселя равен 8 битам — 1 байту. Между базовыми цветами они могут быть распределены так:

2 бита — под красный цвет, 3 бита — под зеленый и 3 бита — под синий.
Интенсивность красного цвета может принимать 22 = 4 значения, интенсивности зеленого и синего цветов — по 23 = 8 значений. Полное число цветов, которые кодируются 8-разрядными кодами, равно: 4 • 8 • 8 = 256 = 28. Снова работает главная формула информатики.
Из описанного правила, в частности, следует:
Обобщение этих частных примеров приводит к следующему правилу. Если размер кода цвета равен b битов, то количество цветов (размер палитры) вычисляется по формуле:
К = 2b.
Величину b в компьютерной графике называют битовой глубиной цвета.
Еще один пример. Битовая глубина цвета равна 24. Размер палитры будет равен:
К = 224 = 16 777216.
В компьютерной графике используются разные цветовые модели для изображения на экране, получаемого путем излучения света, и изображения на бумаге, формируемого с помощью отражения света. Первую модель мы уже рассмотрели — это модель RGB. Вторая модель носит название CMYK.
Цвет, который мы видим на листе бумаги, — это отражение белого (солнечного) света. Нанесенная на бумагу краска поглощает часть палитры, составляющей белый цвет, а другую часть отражает. Таким образом, нужный цвет на бумаге получают путем «вычитания» из белого света «ненужных красок». Поэтому в цветной полиграфии действует не правило сложения цветов (как на экране компьютера), а правило вычитания. Мы не будем углубляться в механизм такого способа цветообразования. Расшифруем лишь аббревиатуру CMYK: Cyan — голубой, Magenta — пурпурный, Yellow — желтый, ЫасК — черный.
Растровая и векторная графика
О двух технологиях компьютерной графики — растровой и векторной — вы знаете из курса информатики основной школы.
В растровой графике графическая информация — это совокупность данных о цвете каждого пикселя на экране. Это то, о чем говорилось выше. В векторной графике графическая информация — это данные, математически описывающие графические примитивы, составляющие рисунок: прямые, дуги, прямоугольники, овалы и пр. Положение и форма графических примитивов представляются в системе экранных координат.
Растровую графику (редакторы растрового типа) применяют при разработке электронных (мультимедийных) и полиграфических изданий. Растровые иллюстрации редко создают вручную с помощью компьютерных программ. Чаще для этой цели используют сканированные иллюстрации, подготовленные художником на бумаге, или фотографии. Для ввода растровых изображений в компьютер применяются цифровые фото- и видеокамеры. Большинство графических редакторов растрового типа в большей мере ориентированы не на создание изображений, а на их обработку.
Достоинство растровой графики — эффективное представление изображений фотографического качества. Основной недостаток растрового способа представления изображения — большой объем занимаемой памяти. Для его сокращения приходится применять различные способы сжатия данных. Другой недостаток растровых изображений связан с искажением изображения при его масштабировании. Поскольку изображение состоит из фиксированного числа точек, увеличение изображения приводит к тому, что эти точки становятся крупнее. Увеличение размера точек растра визуально искажает иллюстрацию и делает ее грубой.
Векторные графические редакторы предназначены в первую очередь для создания иллюстраций и в меньшей степени для их обработки.
Достоинства векторной графики — сравнительно небольшой объем памяти, занимаемой векторными файлами, масштабирование изображения без потери качества. Однако средствами векторной графики проблематично получить высококачественное художественное изображение. Обычно средства векторной графики используют не для создания художественных композиций, а для оформительских, чертежных и проектно-конструкторских работ.
Графическая информация сохраняется в файлах на диске. Существуют разнообразные форматы графических файлов. Они делятся на растровые и векторные. Растровые графические файлы (форматы JPEG, BMP, TIFF и другие) хранят информацию о цвете каждого пикселя изображения на экране. В графических файлах векторного формата (например, WMF, CGM) содержатся описания графических примитивов, составляющих рисунок.
Следует понимать, что графические данные, помещаемые в видеопамять и выводимые на экран, имеют растровый формат вне зависимости от того, с помощью каких программных средств (растровых или векторных) они получены.
Звуковая информация
Принципы дискретизации звука («оцифровки» звука) отражены на рис. 1.11.
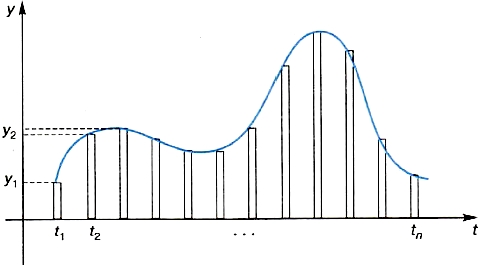
Рис. 1.11. Оцифровка звука (у — интенсивность (уровень) звукового сигнала, t — время)
Ввод звука в компьютер производится с помощью звукового устройства (микрофона, радио и др.)» выход которого подключается к порту звуковой карты. Задача звуковой карты — с определенной частотой производить измерения уровня звукового сигнала (преобразованного в электрические колебания) и результаты измерения записывать в память компьютера. Этот процесс называют оцифровкой звука.
Промежуток времени между двумя измерениями называется периодом измерений — τс. Обратная величина называется частотой дискретизации — 1/τ (герц). Чем выше частота измерений, тем выше качество цифрового звука.
Результаты таких измерений представляются целыми положительными числами с конечным количеством разрядов. Вы уже знаете, что в таком случае получается дискретное конечное множество значений в ограниченном диапазоне. Размер этого диапазона зависит от разрядности ячейки — регистра памяти звуковой карты. Снова работает формула 2i, где i — разрядность регистра. Число i называют также разрядностью дискретизации. Записанные данные сохраняются в файлах специальных звуковых форматов.
Существуют программы обработки звука — редакторы звука, позволяющие создавать различные музыкальные эффекты, очищать звук от шумов, согласовывать с изображениями для создания мультимедийных продуктов и т. д. С помощью специальных устройств, генерирующих звук, звуковые файлы могут преобразовываться в звуковые волны, воспринимаемые слухом человека.
При хранении оцифрованного звука приходится решать проблему уменьшения объема звуковых файлов. Для этого кроме кодирования данных без потерь, позволяющего осуществлять стопроцентное восстановление данных из сжатого потока, используется кодирование данных с потерями. Цель такого кодирования — добиться схожести звучания восстановленного сигнала с оригиналом при максимальном сжатии данных. Это достигается путем использования различных алгоритмов, сжимающих оригинальный сигнал путем выкидывания из него слабослышимых элементов. Методов сжатия, а также программ, реализующих эти методы, существует много.
Для сохранения звука без потерь используется универсальный звуковой формат файлов WAV. Наиболее известный формат «сжатого» звука (с потерями) — MP3. Он обеспечивает сжатие данных в 10 раз и более.
Система основных понятий
Вопросы и задания
- Когда компьютеры начали работать с текстом, с графикой, со звуком?
- Что такое таблица кодировки? Какие существуют таблицы кодиров-ки?
- На чем основывается дискретное представление изображения?
- Что такое модель цвета RGB?
- Напишите 8-разрядный код ярко-синего цвета, ярко-желтого (смесь красного с зеленым), бледно-желтого.
- Почему в полиграфии не используется модель RGB?
- Что такое CMYK?
- Какое устройство в компьютере производит оцифровку вводимого звукового сигнала?
- Как (качественно) качество цифрового звука зависит от частоты дискретизации и разрядности дискретизации?
- Чем удобен формат MP3?

Возможные ответы:
|
43 |
| Глава 2. Информационные процессы |
53 |
| §
7.
Хранение информации
|
53 |
| §
8.
Передача информации
|
59 |
| §
9.
Обработка информации и алгоритмы
|
64 |
| §
10.
Автоматическая обработка информации
|
64 |
| §
11.
Информационные процессы в компьютере
|
74 |
| Глава 3. Программирование обработки информации |
86 |
| §
12.
Алгоритмы и величины
|
86 |
| §
13.
Структура алгоритмов
|
92 |
| §
14. Паскаль — язык структурного программирования
|
99 |
| §
15.
Элементы языка Паскаль и типы данных
|
105 |
| §
16.
Операции, функции, выражения
|
110 |
| §
17.
Оператор присваивания, ввод и вывод данных
|
116 |
| §
18.
Логические величины, операции, выражения
|
123 |
| §
19.
Программирование ветвлений
|
132 |
| §
20.
Пример поэтапной разработки программы решения задачи
|
136 |
| §
21.
Программирование циклов
|
142 |
| §
22.
Вложенные и итерационные циклы
|
150 |
| §
23.
Вспомогательные алгоритмы и подпрограммы
|
155 |
| §
24.
Массивы
|
163 |
| §
25.
Организация ввода и вывода данных с использованием файлов
|
169 |
| §
26.
Типовые задачи обработки массивов
|
175 |
| §
27.
Символьный тип данных
|
181 |
| §
28.
Строки символов
|
185 |
| §
29.
Комбинированный тип данных
|
190 |
| Практикум |
197 |
|
Практические работы к главе 1 «Информация»
|
197 |
|
Практические работы к главе 2 «Информационные процессы»
|
215 |
|
Практические работы к главе 3 «Программирование обработки информации»
|
231 |
|
Ответы к заданиям практических работ
|
263 |
|